Ответ на вопрос: «Горное давление. Напряженное состояние горных пород в массиве и в околоскважинных зонах».
Горное давление, обуславливается весом пород, тектоническими силами, пластовым давлением и термическими напряжениями, возникающим под влиянием тепла земных недр. В результате воздействия на породу комплекса упомянутых сил, элемент породы, выделенный из массива, находится в сложном напряженном состоянии, результирующие векторы не перпендикулярны к его граням.
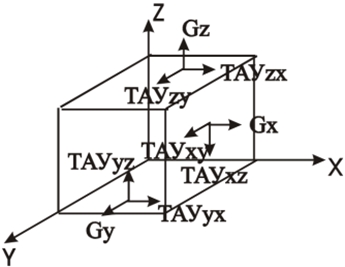
Разлагая эти результирующие, имеем три компоненты напряжений — одна нормальная G, направлена перпендикулярно к грани кубика, и две касательные τ. Условие состояния относительного покоя:
Gy ≅ Gx ≅ Gz; τxy = τyx; τxz = τzx; τyz = τzy
Нормальные и касательные напряжения, действующие на элемент породы, вызывают соответствующие деформации его граней. G — сжатие и растяжение (εx, εy и εz). τ — сдвиг граней (деформация сдвига обычно измеряется углами сдвига).
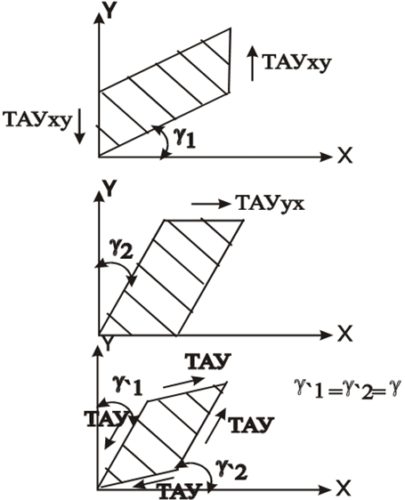
На верхнем рисунке показан сдвиг грани элемента при влиянии одной пары касательных напряжений xy, на среднем рисунке сдвиг под влиянием другой пары yx. В результате наложения этих сдвигов деформация грани будет иметь вид, изображенный на нижнем рисунке. В результате сдвига прямой угол грани уменьшится на сумму этих углов: γxy = γ1' + γ2'.
Если породы однородны γxy = 2γ. В случае полностью изотропного тела связь между напряжениями и деформациями можно выразить следующими уравнениями, которые согласно закону Гука имеют вид:
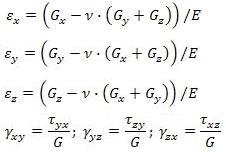
где Е — модуль продольной упругости (модуль Юнга);
ν — коэффициент Пуассона (Тела деформируются по направлению действия силы. При этом происходят поперечные деформации, перпендикулярные к направлению силы, т.е. тело расширяется при сжатии или сужается при растяжении. Поперечная деформация εп составляет часть продольной ε: εп = -ε · ν);
G — модуль сдвига.
Связь между ними выражается следующими формулами:
![]()
До нарушения условий залегания пород скважиной внешнее давление от действия собственной массы вышележащих пород и возникающие в породе ответные напряжения находятся в условиях равновесия.
Составляющие имеют следующие значения:
По вертикали: σz = ρ · g · H,
где σz — вертикальная составляющая напряжений;
ρ — плотность породы;
H — глубина залегания пласта.
По горизонтали: σy = σx = n · ρ · g · H = n · σz
где n-коэффициент бокового распора; для пластичных горных пород n = 1; для упруго-пластичных горных пород подверженным определенным осложнениям в тектоническом отношении n → 0; для хрупких и хрупко-пластичных n = 0,3-0,7.
Допустим, что горизонтальные составляющие σy = σx и не оказывает особое влияние на напряженное состояние горных пород и не учитывается пластичность горных пород εx = εx = 0; σx = σx = σz · (ν / (1 — ν)); n = ν / (1 — ν).
Напряженное состояние горных пород в ОЗП
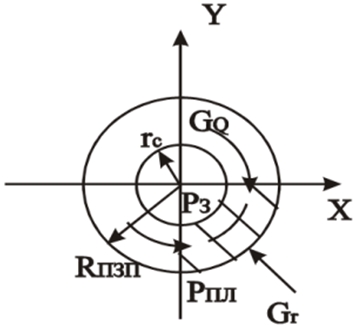
GQ — тангенциальная составляющая; Gr — радиальная составляющая (нормального напряжения). Gr = Pз (Pз — забойное давление).
GΘ = 2 · n · ρ · g · H
Т.е. на стенке скважины могут действовать окружные сжимающие напряжения, которые при Pз = 0 достигают двойного значения горного давления.
Это означает, что при наличии пород недостаточной прочности в призабойной зоне возможно их разрушение под действием тангенциальных напряжений и ухудшение фильтрационных свойств пород вследствие их сжатия под влиянием этих нагрузок. Следовательно, стенки ствола скважины будут устойчивы, если:
GΘ = 2 · n · ρ · g · H < σсж,
где σсж – предел прочности породы при двухосном сжатии.